Matemáticas II

"CONCEPTOS Y CLASIFICACIÓN DE POLÍGONOS"

Polígonos

Los polígonos son figuras cerradas formadas por varios segmentos de recta a los que llamamos lados.

Clasificación de polígonos

Según sus lados
Los polígonos reciben diferentes nombres según el número de lados que poseen. Te invitamos a conocer el nombre de los polígonos de hasta 15 lados:


Según la medida de sus lados
Los polígonos pueden ser regulares e irregulares:
Son polígonos regulares los que tienen todos sus lados y ángulos congruentes, es decir tienen la misma medida.



Irregulares son aquellos en que al menos uno de los lados tiene diferente medida o sus ángulos son diferentes.



Según sus ángulos
Los podemos clasificar en cóncavos o convexos:
Un polígono será convexo, si todos sus ángulos son menores de 180°, por lo tanto, si determinamos dos puntos en su interior y los unimos con un segmento, éste siempre quedará en su interior.



Y será cóncavo, si al menos uno de sus ángulo mide más de 180°. Como muestra la figura, no todos los segmentos trazados entre dos puntos quedarán en su interior.

"TEOREMAS DE ÁNGULOS EN LOS POLÍGONOS

Y EJEMPLOS"

Teorema No. 1. La suma de los ángulos interiores de un polígono es igual a 180° (n-2), donde “n” es el lado, o mejor, el número de lados del polígono.

EJEMPLO:

• Calcular la suma de los ángulos interiores de un pentágono regular.

Suma de ángulos interiores    = 180(n-2)

Suma de ángulos interiores      = 180(5-2)

Suma de ángulos interiores      = 180(3)

Suma de ángulos interiores      = 540°.

Teorema No. 2. Si se quiere calcular el ángulo interior de algún polígono, éste debe ser regular, el valor de cada uno de sus ángulos es el mismo y es igual a la división de la suma de los ángulos interiores entre “n”.

Ángulo interior = 180(n-2)

                               n

EJEMPLO:

• Calcular el ángulo interior de un pentadecágono (15 lados) regular.

Ángulo interior = 180(n-2) = 180(15-2) = 180(13) = 2340 = 156°

                                 n                15             15           15

Teorema No. 3. La suma de los ángulos exteriores de un polígono es de 360°.

Ángulo exterior = 360°

                                 n

EJEMPLO:

 • Calcular el ángulo exterior de un triángulo.

Ángulo exterior = 360° = 360° = 120°

                              n          3

 Teorema No. 4. El número de diagonales que pueden trazarse desde los vértices de un polígono es igual al producto de n(n-3) y todo ello dividido entre 2.

# de / = n(n-3)

              2

EJEMPLO:

• Calcular el número de diagonales de un pentágono regular.

# de / = n(n-3) = 5(5-3) = 5(2)= 10 = 5 diagonales.

               2             2          2       2

 "LUGARES GEOMÉTRICOS RELACIONADOS CON LA CIRCUNFERENCIA"

Lugar geométrico (L.G) es el conjunto de todos los puntos del plano que cumplen con una condición dada. Es decir, todo L.G. presenta las siguientes características:

1.       es un conjunto de puntos.

2.       todos los puntos cumplen con una misma propiedad que lo caracteriza.

El L.G. puede ser una linea curva, una recta, un plano, una superficie curva, etc. y a veces el mismo conjunto de puntos puede satisfacer más de una propiedad.

Iniciemos determinando los puntos de un plano que están a una distancia  dada "a" de un punto P del mismo plano.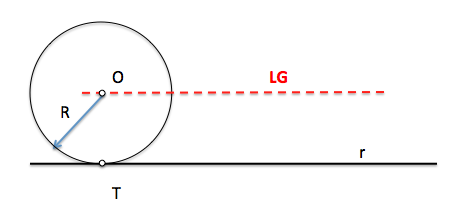 

Vemos que los puntos que cumplen con esta condición son los que forman parte de la circunferencia de centro P y radio a.

Vemos que los puntos que cumplen con esta condición son los que forman parte de la circunferencia de centro P y radio a.

Luego, la circunferencia es el L.G. de todos los puntos del plano que están a una distancia dada de un punto dado.

 Lugares geométricos más comunes

    * La circunferencia de centro P y radio r, es el L.G. de todos los puntos del plano que están a la distancia r del punto P.

 *  La circunferencia de centro P y radio r, es el L.G. de todos los centros de circunferencias de radio r que pasan por el punto dado P.

*  La perpendicular levantada en el punto medio del segmento AB es el L.G. de todos los puntos del plano que equidistan de los puntos A y B.

* La perpendicular levantada en el punto medio del segmento AB es el L.G. de todos los centros de las circunferencias que pasan por los puntos A y B.

*  Las paralelas a la distancia d de una recta dada L representan el L.G. de todos los puntos del plano que se encuentran a la distancia d de la recta L.

*  Las paralelas a la distancia d de una recta dada L representan el L.G. de los centros de todas las circunferencias de radio d tangentes a la recta dada L.

*  La paralela media a dos rectas paralelas dadas y  representa el L.G. de todos los puntos del plano equidistantes de las rectas y 

*  La paralela media a dos rectas paralelas dadas y  representa el L.G. de los centro de todas las circunferencias tangentes a las paralelas dadas y 

*  La bisectriz de un ángulo dado es el L.G. de todos los puntos del plano que se encuentran equidistantes de los lados del ángulo.

*  La bisectriz de un ángulo dado es el L.G. de los centros de todas las circunferencias tangentes a los lados del ángulos.

*  Las bisectrices de los ángulos que forman dos rectas dadas y  al intersectarse, representan el L.G. de todos los puntos del plano equidistantes de las rectas y 

*  Las bisectrices de los ángulos que forman dos rectas dadas y  al intersectarse, representan el L.G. de todos los centros de las circunferencias tangentes a las rectas y .

*  Dadas dos circunferencias concéntricas, la circunferencia concéntrica con las anteriores y de radio igual a la semisuma de los radios dados es el L.G. de todos los puntos del plano equidistantes de las circunferencias dadas.

*  Dadas dos circunferencias concéntricas, la circunferencia concéntrica con las anteriores y de radio igual a la semisuma de los radios dados es el L.G. de los centros de todas las circunferencias tangentes a las circunferencias dadas.

*  El arco capaz de a construído sobre la cuerda BC, es el L.G. de todos los terceros vértices de los triángulos que tienen el lado BC común y el ángulo opuesto igual a  a .

*  La circunferencia que tiene por diámetro el segmento AB es el L.G. de los vértices correspondientes al ángulo recto de todos los triángulos rectángulos de hipotenusa AB. 

"TEOREMAS DE ÁNGULOS DENTRO Y FUERA DE LA CIRCUNFERENCIA" 

1 Ángulo central

El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.

2 Ángulo inscrito

El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.
Mide la mitad del arco que abarca.

3 Ángulo semi-inscrito

El vértice de ángulo semiinscrito está en la circunferencia, un lado secante y el otro tangente a ella.
Mide la mitad del arco que abarca.

4 Ángulo interior

Su vértice es interior a la circunferencia y sus lados secantes a ella.
Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.

5 Ángulo exterior

Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:

Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:

EJEMPLOS:

15.146  ¿Cuánto vale el ángulo cuyo vértice señalamos con X?. Razona la respuesta:

Respuesta: X=70º30’. Se trata de un ángulo inscrito y vale la mitad del arco que abarcan sus lados, es decir, la mitad del ángulo central.

15.147 ¿Qué valor tiene X en la figura siguiente? Razónala.

Respuesta: X=31º. Mismo razonamiento del problema anterior.

15.148   Halla el valor de X en la figura siguiente:

Respuesta: X=62º por ser ángulo central y tener el doble del valor del ángulo inscrito cuyos lados abarcan el mismo arco.

15.149 ¿Cuántos grados vale el ángulo X?

Respuesta: X=135º
Solución:

El ángulo es inscrito y sus lados abarcan el arco que corresponde al ángulo central de 270º, luego X valdrá la mitad del ángulo central, es decir,

15.150 ¿Cuánto vale el ángulo X de la figura siguiente y cuál la longitud del arco que abarcan sus lados?

Respuesta: X= 136º30’: longitud del arco =

4) Ángulo interior: Un ángulo interior es el que tiene su vértice en un punto interior cualquiera de la circunferencia y sus lados son secantes a ella:

El ángulo es un ángulo interior del que a continuación vamos a deducir el valor del arco que abarcan sus lados..

En primer lugar prolongamos los lados y :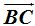

Ahora unimos los puntos A y D:

Si te fijas bien, el ángulo es un ángulo inscrito y vale la mitad del central la longitud del arco que le corresponde es :

Ves que el ángulo vale 73º, es decir, la mitad del ángulo central que mide 146º, abarcando los lados de ambos ángulos el mismo arco.

Podemos decir que

El ángulo también es un ángulo inscrito y le corresponderá el arco

Escribiremos la igualdad

En el triángulo el ángulo en 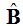verás que es un ángulo exterior, por lo tanto, vale la suma de los interiores no adyacentes a él:

   

"TEOREMAS DE MEDIAS PROPORCIONALES"

Junto con los conceptos de potencia, la geometría del triángulo rectángulo permite resolver la obtención de medias proporcionales mediante los teoremas denominados de la altura y del cateto 

.

Antes de enunciar y deducir estos teoremas, recordemos algunos conceptos básicos de proporcionalidad para entender qué es lo que podemos resolver con las construcciones derivadas de estos modelos geométricos.

Cuarto proporcional

Dada la relación matemática x/a =b/c llamamos cuarto proporcional al valor de x, es decir

x=a*b/c

Tercero proporcional

Dada la relación matemática x/a = a/b llamamos tercero proporcional al valor de x, es decir

x=a*a/b

Media proporcional

Dada la relación matemática x/a=b/x llamamos media proporcional al valor de x, es decir

x= raíz cuadrada de a*b

En los tres casos definidos, la relación puede provenir de modelos basados en la semejanza y por lo tanto de relaciones obtenidas aplicando el teorema de Thales.

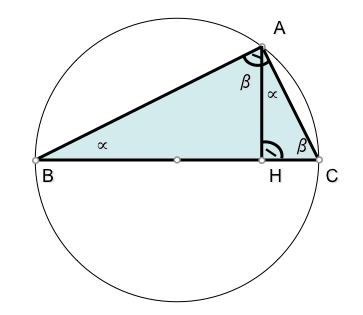
Geometría del triángulo rectángulo

Podemos obtener un triángulo rectángulo utilizando como hipotenusa un diámetro de una circunferencia, y como vértice opuesto un punto de la misma, ya que determina un arco capaz de 90 grados sobre dicho diámetro.

Si obtenemos la altura h del triángulo desde el ángulo recto (vértice A) y determinamos su intersección H con la hipotenusa (pie de la altura) podemos determinar tres triángulos rectángulo semejantes:

• ABC
• HAC
• HBA

Teoremas de la altura y del cateto

Aplicando Thales a estos tres triángulos podemos obtener las siguientes relaciones:

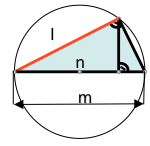
Teorema del cateto

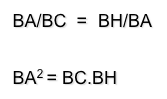
El cateto de un triángulo rectángulo es media proporcional entre la hipotenusa y la proyección de dicho cateto sobre la hipotenusa.

l*l=m*n

Teorema del cateto

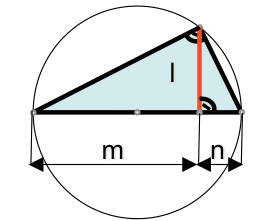
Teorema de la altura

La altura de un triángulo rectángulo medida sobre su hipotenusa es media proporcional entre los dos segmentos en que la divide.

l*l=m*n

PROBLEMAS DE ÁREAS Y PERÍMETROS

1. Un granjero desea hacer un corral para guardar sus animales, el terreno del cual dispone se presta para construir el corral de distintas formas, él analiza las siguientes con las medidas que se adjuntan considerando que cuenta con 60 m de alambre y en cuál se cubre mayor superficie y por lo mismo cuál puede albergar a mayor cantidad de animales, en cuál se podría aprovechar más la superficie de acuerdo a la forma.

Todas las formas tienen de perímetro 60 metros

De 20 m en cada lado

Con lados de 15 m

El lado menor de 10 m y el mayor de 20 m

De perímetro aproximado a 60 m

• Analiza las posibilidades de cada corral de acuerdo a los criterios entregados y agregan otra posibilidad a la forma del corral.
• Propon la forma que puede tener el corral y fundamentan tu elección

2. Completa la siguiente tabla:

 

radio	perímetro	área
1 cm
2 cm
	16p
4 cm
		9p
6 cm
10 cm
	24p

3. Si el radio en una circunferencia se aumenta, cómo aumenta el perímetro correspondiente? ¿Es posible afirmar que la relación entre el radio y el perímetro correspondiente es proporcional? ¿Por qué? 4. Si el radio en una circunferencia se aumenta, cómo aumenta el área correspondiente? ¿Cómo se puede caracterizar el aumento del área del círculo? ¿Es posible afirmar que la relación entre el radio y el área correspondiente es proporcional? ¿Por qué?
5. La tierra está a una distancia del sol de 155 millones de km. aproximadamente. La trayectoria de la Tierra alrededor del Sol es casi circular.

• ¿Qué distancia recorremos "en órbita" alrededor del Sol cada año?
• Para realizar los cálculos ¿Qué valor es conveniente usar para p ? ¿Por qué?
• ¿Cuál sería una buena aproximación de la velocidad de la Tierra en su órbita?

6. ¿Cuál es el perímetro de la circunferencia si el rectángulo está inscrito en la circunferencia y su lado mayor mide 12 cm y el menor 9 cm?

5. En parejas de trabajo, resuelven las siguientes situaciones, evalúan su respuesta y presentan su desarrollo

1. En el dibujo, no realizado a escala, se presenta un tablero para aficionados de tiro al blanco con 3 zonas de tiro.

En teoría, si el tablero está bien construido el jugador debería tener la misma probabilidad de acertar en cada una de las secciones del tablero.

• ¿Cómo se puede saber que efectivamente el diseño da las mismas posibilidades de ubicar una plumilla en cada sector? ¿Qué cálculo que involucre el diseño permite esta certeza?
• En el caso que el radio del círculo interior sea 12 cm. ¿Cuál debería ser el área de cada anillo?
• Imaginan que cada anillo de color pertenece a un círculo (con igual centro al más pequeño). Si el círculo interior tiene de radio 12 cm, ¿Cuál debería ser área de cada uno de los círculos más grandes, de manera que el diseño del tablero sea el correcto?

Expresan el área de cada círculo de al menos tres maneras

• ¿Cuál debería ser el radio de cada uno de los círculos antes señalados? Presentan la respuesta : calculando la raíz con la calculadora y sin calcular la raíz

6. Las piezas de cuero tienen diferentes tamaños y formas, sin embargo la mayoría se acerca a una forma rectangular.

Un artesano compró varias piezas, en una está realizando los cortes para las bases de un cubilete de cacho, que se sabe tienen forma circular. El radio de cada pieza es de 3 cm y el tamaño de la pieza es aproximadamente de 1 metro por 80 cm y su valor es de 30 mil pesos

¿Cómo sería recomendable disponer las bases circulares de manera que se aproveche al máximo la pieza de cuero? Hacen un dibujo esquemático de la distribución y explican por qué es la forma en la cual se aprovecha mejor la pieza. ¿Cuántas bases circulares alcanza a obtener con ella?

¿Cuánto cuero se pierde de la pieza completa? Aproximadamente a cuánto dinero equivale esta pérdida en esta pieza de cuero?